Some concepts turn up again and again in A-level biology. Taking a little time to ensure you really understand these key concepts from the start can save a lot of effort overall.

Surface area to volume ratio (SA:V) is vital for understanding a wide range of topics including transport across cell membranes, gas exchange, digestion, heat exchange, and mass transport. SA:V explains why the inner membrane of a mitochondrion is folded, why elephants have big ears, and why jellyfish don’t need blood vessels.

How confident are you in calculating this value and understanding its significance?

What are surface-area-to-volume ratios?

"Microvilli-Duodenum" by Wbensmith is licensed under CC BY-SA 3.0.

This topic is all about how changing the shape or volume of something affects its surface area. It’s not as simple as many people think: doubling the volume of ice-cream in a choc-ice doesn’t double the amount of chocolate needed to cover it.

Surface areas are really important in biology. And so the shapes and volumes of things including organelles, cells, and organs are often optimised with respect to surface area. Whenever you see a weird folded or worm-shape structure, think about SA:V.

Surface area to volume ratio (SA:V) is a value calculated by dividing a thing’s surface area by its volume. It is a single number that tells you about the relationship between the two input values.

To be precise: SA:V tells you how much surface area there is per unit of volume.

How to calculate SA:V (it’s not hard, you just divide)

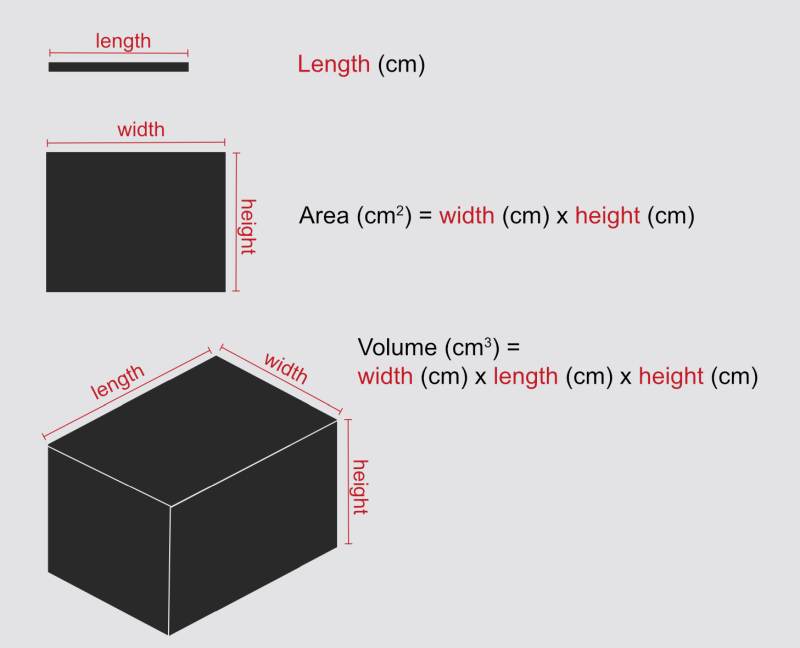
Quick maths refresher

You will need to think about length, area, and volume and understand their units. Here’s a reminder for cuboids:

Image showing how the area of a square is calculated as width x height, with a squared unit, and volume of a cuboid is calculated by length x width x height, with a cubed unit

Simple example

Imagine a cube where every edge is 1 cm long.

Each square face of the cube has a surface area of 1 cm x 1 cm = 1 cm^2
Cubes have six faces, so the total surface area is 6 x 1 cm^2 = 6 cm^2
The volume of the cube is 1 cm x 1 cm x 1 cm = 1 cm^3
SA:V = surface area / volume. In this example that’s 6 cm^2 / 1 cm^3 = 6 cm^-1

Notice the funny unit there. You’ve divided cm^2 by cm^3 so they don’t cancel out perfectly.
But does it matter what this unit is? Let’s try it using the same cube but measuring it in millimetres.

Each square face of the 1 cm cube has a surface area of 10 mm x 10 mm = 100 mm^2
Cubes have six faces, so the total surface area is 6 x 100 mm^2 = 600 mm^2
The volume of the cube is 10 mm x 10 mm x 10 mm = 1000 mm^3
SA:V = surface area / volume. Using millimetres that’s 600 mm^2 / 1000 mm^3 = 0.6 mm^-1

1 mm is 1/10 of 1 cm and the SA:V calculated in mm is 1/10 that of the value calculated in cm. If you are comparing SA:V values, make sure they have the same unit.

Of course you don’t find a lot of cubes in nature. In exams they might simplify cells or other bodies to be imagined as spheres of a known radius, and give you equations for you to calculate the surface area and volume. And there are much weirder shapes to think about too. But before we get to all that …

How does SA:V change as things increase in scale?

An image of a single stone cube, and then eight similar cubes assembled into a larger cube, as described in the text. They are sat on a wooden chess board for no reason.

We know the 1 cm cube has a SA:V of 6 cm^-1.

So, what if we get a handful of these 1 cm cubes and stick them together to make a scaled-up cube where every edge is 2 cm long? (See picture). How will the SA:V of this new structure compare? It’s still a cube, after all; it’s just a bit bigger.

2-cm cube:

Each square face of the assembled cube has a surface area of 2 cm x 2 cm = 4 cm^2
Cubes have six faces, so the total surface area is 6 x 4 cm^2 = 24 cm^2
The volume of the assembled cube is 2 cm x 2 cm x 2 cm = 8 cm^3
SA:V = surface area / volume. In this example that’s 24 cm^2 / 8 cm^3 = 3 cm^-1

The larger cube’s SA:V is only half that of the unit cube!

SA:V is surface area divided by volume. Higher values of SA:V mean there is more surface area for each unit of volume, and lower values of SA:V mean there is less surface area for each unit of volume.

So our 2 cm cube has less surface area per unit volume than the 1 cm cube did.

The larger cube has a lower SA:V. And if you work out the numbers for an even bigger one, you’ll get an even lower SA:V.

This makes sense. To build the 2 cm cube, you stack eight 1 cm cubes together. By doing this, you bury some of their faces within the structure. You end up with the same volume as eight individual 1-cm cubes, but you have reduced the surface area that is exposed to the outside world.

Also, if you look carefully at the picture, you’ll see that each cube in the assembled structure has half of its faces buried. So there’s only half the surface area per unit volume compared to the single cube. And so it makes sense that the SA:V is half what it was for the single cube.

Each small cube is only showing three of its six faces. So for each 1 cm^3 volume (ie for each small cube) there is 3 cm^2 surface area exposed, giving us an overall SA:V of 3 cm^-1.

Key concept: as size increases, SA:V decreases. This is a good thing to explicitly state in any question about SA:V and size, where the shape stays the same.

Try it: calculate SA:V for a 3 cm x 3 cm cube. What value do you guess you might get? And what is the actual value?

Why size matters

"Zygote" by Nina Sesina is licensed under CC BY-SA 4.0.

Imagine you are a single cell (well, you were once, don’t you remember?).

Your cell membrane is your connection with the outside world. Through it you take in nutrients, water and other necessary things. And you expel your waste through it.

This membrane is your surface; you have as much cell membrane as you have surface area.

Meanwhile, inside the cell membrane you have cytoplasm, organelles, etc. In this region you are busily metabolising and catabolising molecules. You can measure this region as your volume.

Question: can you take in enough nutrients, and expel enough waste, to keep up with your metabolism?
More-important question: if you grow bigger, will this still be true?

*Valonia ventricosa* aka Sailors eyeball - a single cell that can grow up to 5 cm in diameter. But … how???

As a cell grows larger its SA:V falls. This is just like we saw with scaling up the cubes above. The growth of the cell’s surface area (cell membrane) just can’t keep up with the growth of its volume (where the metabolism is). This means there will be a point at which there just isn’t enough cell membrane (surface area) to transport everything that needs to be transported, limiting the cells ability to function.

This is one reason why cells tend to be pretty small!

But … wait a minute, what about the freakish cell in this photo? A shiny, bright green, single-celled alga that can get up to 5 cm in diameter. A single cell! Charmingly known as ‘sailors’ eyeballs’.

But how can one cell possibly be so large? Isn’t its SA:V ridiculously low? (Spoiler: yes it is). How can it transport everything it needs with such a low SA:V? Well, it has a trick …

Shape matters

This giant cell is cheating. Inside, all the metabolic activity is limited to an area very close to its cell membrane. Nearly all of the cell’s interior is filled up by one giant vacuole that pushes all the interesting stuff out to the region next to the membrane. So there isn’t nearly as much metabolism going on in there as you might imagine from its total volume. If you re-calculated its SA:V ignoring the volume inside its vacuole, you’d get a much more sensible number. It also has multiple nuclei spread throughout its cytoplasm.

In exams, questions are usually about solid spheres or cuboids. We’ve looked at cuboids, so let’s look at spheres.

Spheres

If you have to calculate for spheres, they will give you the equations you need to calculate volume and surface area. So don’t worry about remembering these.

Volume of a sphere = 4/3 x π x r^3
Surface area of a sphere = 4 x π x r^2

So, if you have a sphere of radius 1 cm (remember this is just the distance from the centre to the outside, so the whole thing is 2 cm across):

The surface area is 4 x π x r^2. If r = 1, r^2 = 1. So the surface area is 4 x 3.14 x 1 = 12.6 cm^2

The volume is 4/3 x π x r^3. If r = 1, r^3 = 1. So the volume is 4/3 x 3.14 x 1 = 4.19 cm^3
SA:V = surface area / volume. In this example that’s 12.6 cm^2 / 4.19 cm^3 = 3 cm^-1

This is the same SA:V as the 2-cm cube!

That important phrase “as size increases, SA:V decreases”, is talking about increasing the size of something while keeping the same shape overall. Shape is also really important!

Spheres have the lowest possible surface area for their volume. This is one of the reasons that nature likes them. For example, bubbles are spheres because surface tension pulls their surface in to minimise its area.

Stretching out

If a cell needs to grow to large dimensions but also needs to keep a high SA:V, it needs to avoid being a sphere. More-complex shapes will always have higher SA:V.

Consider neurons. You have a single neuron that reaches from your big toe to your spine. A single cell over a metre long! But these neurons are definitely not spheres. They are very skinny.

Question: what happens to SA:V when you make long/thin shapes?

Let’s go back to the 1 cm cubes. The 1 cm cube had a SA:V of 6. And the 2 cm cube had a SA:V of 3.

Image of the same eight cubes as were used to make the 2-cm cube, but now arranged flat on the table as a rectangle of 2 x 4 cubes.

The 2 cm cube had a volume of 8 cm^3 : it was made out of eight small cubes. Let’s take those eight small cubes and rearrange them into the shape of a flatworm: a rectangular block of 2 cm x 4 cm x 1 cm (see picture above).

The upper and lower faces of this shape each have a surface area of 8 cm^2
The two long sides of this shape each have a surface area of 4 cm^2
The two ends of this shape each have a surface area of 2 cm^2
The total surface area is (2 x 8 cm^2) + (2 x 4 cm^2) + (2 x 2 cm^2) = 28 cm^2 (the 2 cm cube had 24 cm^2)
The volume of the assembled cube is 2 cm x 4 cm x 1 cm = 8 cm^3 (ok that isn’t a surprise)
SA:V = surface area / volume. In this example that’s 28 cm^2 / 8 cm^3 = 3.5 cm^-1 (the 2 cm cube was 3 cm^-1)

Rearranging it from a 2 cm cube to a flatworm of the same volume has increased its SA:V.

Ok so let’s push it even further and turn it into a long worm.

The same eight cubes, but this time all in one long line making a long skinny shape

The upper and lower faces of this shape each have a surface area of 8 cm^2
The two long sides of this shape each have a surface area of 8 cm^2
The two ends of this shape each have a surface area of 1 cm^2
The total surface area is (2 x 8 cm^2) + (2 x 8 cm^2) + (2 x 1 cm^2) = 34 cm^2
The volume of the assembled cube is 1 cm x 8 cm x 1 cm = 8 cm^3 (no surprise)
SA:V = surface area / volume. In this example that’s 28 cm^2 / 8 cm^3 = 4.25 cm^-1 (the 2 cm cube was 3 cm^-1)

Your neurons can be really, really long because they’re also skinny, because that means they still have a really high SA:V.

And of course this works for whole animals too. Many small animals lack blood vessels and rely on molecules simply diffusing through their bodies. They need high surface area for transport and they also need every part of their interior to be not-to-far from that surface. This is (one of) the reasons we don’t have truly-giant insects: they are limited by their ability fo transport things to/from the outside world. Sponges and jellyfish also lack blood vessels and rely on diffusion.

Humans, alongside other larger animals, have much lower SA:V and suffer from low diffusion rates. So we need specialised structures to aid exchange and transport.

Maximising SA:V

Structures that are involved in transport and exchange rely upon having very high surface areas of membrane across which transport can take place. To maximise exposed surface area, structures are folded, or shaped into fingers, or branches.

In the human body, you find extremely high SA:V ratio in specialised structures including:

Gut - the gut wall has microvilli, finger-like structures that extend into the lumen. These increase surface area for absorption of water and nutrients
Lungs - the lungs have many branches terminating in tiny alveoli offering a very high surface area for gas exchange.
Capillaries - capillaries have much higher SA:V than arteries or veins. This offers a higher surface area for transporting things between the blood and tissue fluids. It also increases fluid resistance, which is important to keep the blood moving forward.
Red blood cells have a biconcave shape that increases their SA:V allowing better gas exchange with the blood plasma.

In other organisms, the shapes of structures like leaves, chloroplasts, gills, root hairs, and fungal hyphae, among many other examples, are similarly optimised to maximise surface area to volume ratios.

Folded membranes

You also find folded membranes used as a way to squeeze a load of membrane into a small space. Eg:

Mitochondria have a highly folded inner membrane that offers more surface area to embed the enzymes and proteins involved in oxidative phosphorylation, so that more ATP can be produced.

Golgi apparatus and endoplasmic reticulum are similarly folded to maximise their surface area.

Thermoregulation

The person on the left is sat with their knees to their chest, hugging their legs with their head low. The person on the right is stood up straight with their legs slightly apart and arms held away from their body. — Who is is feeling cold, and who is feeling hot?

Body surfaces also exchange heat with the environment.

We naturally change our SA:V when we get hot or cold by changing the position of our limbs and body. Which of the people in the image has the highest SA:V? Which person is cold, and which is hot?

Dogs increase their surface area by opening their mouths when hot and panting (passing air over their wet surfaces to lose heat through evaporation). Cats form neat loafs when cold but sprawl dramatically across the floor when hot.

Organisms’ entire body shape will also be related to their thermoregulatory needs.

Animals that need to lose heat from their bodies usually have a higher SA:V, and animals that need to conserve heat usually have a lower SA:V. This is why elephants have such huge ears (more surface area from which to lose heat) and why animals from cold environments tend to be more spherical than those from hot climates.

This article was written by Dr Jenny Shipway with guidance from Tom Whitburn